travelling salesman example

• Interview Problems on Graph
• Practice Graph
• MCQs on Graph
• Graph Tutorial
• Graph Representation
• Graph Properties
• Types of Graphs
• Graph Applications
• BFS on Graph
• DFS on Graph
• Graph VS Tree
• Transpose Graph
• Dijkstra's Algorithm
• Minimum Spanning Tree
• Prim’s Algorithm
• Topological Sorting
• Floyd Warshall Algorithm
• Strongly Connected Components
• Advantages & Disadvantages

Traveling Salesman Problem (TSP) Implementation

Travelling Salesman Problem (TSP) : Given a set of cities and distances between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point.  Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle.  For example, consider the graph shown in the figure on the right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. The problem is a famous NP-hard problem. There is no polynomial-time known solution for this problem.   

Examples: 

In this post, the implementation of a simple solution is discussed.

• Consider city 1 as the starting and ending point. Since the route is cyclic, we can consider any point as a starting point.
• Generate all (n-1)! permutations of cities.
• Calculate the cost of every permutation and keep track of the minimum cost permutation.
• Return the permutation with minimum cost.

Below is the implementation of the above idea 

Time complexity:  O(n!) where n is the number of vertices in the graph. This is because the algorithm uses the next_permutation function which generates all the possible permutations of the vertex set.  Auxiliary Space: O(n) as we are using a vector to store all the vertices.

Similar Reads

• NP Complete

Please Login to comment...

Improve your coding skills with practice.

What kind of Experience do you want to share?

• Career Schools - Jaipur - Jodhpur
• Apply as Mentor

DSA Tutorial

Linked lists, stacks & queues, hash tables, shortest path, minimum spanning tree, maximum flow, time complexity, dsa reference, dsa examples, dsa the traveling salesman problem.

The Traveling Salesman Problem

The Traveling Salesman Problem states that you are a salesperson and you must visit a number of cities or towns.

Rules : Visit every city only once, then return back to the city you started in.

Goal : Find the shortest possible route.

Except for the Held-Karp algorithm (which is quite advanced and time consuming, (\(O(2^n n^2)\)), and will not be described here), there is no other way to find the shortest route than to check all possible routes.

This means that the time complexity for solving this problem is \(O(n!)\), which means 720 routes needs to be checked for 6 cities, 40,320 routes must be checked for 8 cities, and if you have 10 cities to visit, more than 3.6 million routes must be checked!

Note: "!", or "factorial", is a mathematical operation used in combinatorics to find out how many possible ways something can be done. If there are 4 cities, each city is connected to every other city, and we must visit every city exactly once, there are \(4!= 4 \cdot 3 \cdot 2 \cdot 1 = 24\) different routes we can take to visit those cities.

The Traveling Salesman Problem (TSP) is a problem that is interesting to study because it is very practical, but so time consuming to solve, that it becomes nearly impossible to find the shortest route, even in a graph with just 20-30 vertices.

If we had an effective algorithm for solving The Traveling Salesman Problem, the consequences would be very big in many sectors, like for example chip design, vehicle routing, telecommunications, and urban planning.

Checking All Routes to Solve The Traveling Salesman Problem

To find the optimal solution to The Traveling Salesman Problem, we will check all possible routes, and every time we find a shorter route, we will store it, so that in the end we will have the shortest route.

Good: Finds the overall shortest route.

Bad: Requires an awful lot of calculation, especially for a large amount of cities, which means it is very time consuming.

How it works:

• Check the length of every possible route, one route at a time.
• Is the current route shorter than the shortest route found so far? If so, store the new shortest route.
• After checking all routes, the stored route is the shortest one.

Such a way of finding the solution to a problem is called brute force .

Brute force is not really an algorithm, it just means finding the solution by checking all possibilities, usually because of a lack of a better way to do it.

Speed: {{ inpVal }}

Finding the shortest route in The Traveling Salesman Problem by checking all routes (brute force).

Progress: {{progress}}%

n = {{vertices}} cities

{{vertices}}!={{posRoutes}} possible routes

Show every route: {{showCompares}}

The reason why the brute force approach of finding the shortest route (as shown above) is so time consuming is that we are checking all routes, and the number of possible routes increases really fast when the number of cities increases.

Finding the optimal solution to the Traveling Salesman Problem by checking all possible routes (brute force):

Using A Greedy Algorithm to Solve The Traveling Salesman Problem

Since checking every possible route to solve the Traveling Salesman Problem (like we did above) is so incredibly time consuming, we can instead find a short route by just going to the nearest unvisited city in each step, which is much faster.

Good: Finds a solution to the Traveling Salesman Problem much faster than by checking all routes.

Bad: Does not find the overall shortest route, it just finds a route that is much shorter than an average random route.

• Visit every city.
• The next city to visit is always the nearest of the unvisited cities from the city you are currently in.
• After visiting all cities, go back to the city you started in.

This way of finding an approximation to the shortest route in the Traveling Salesman Problem, by just going to the nearest unvisited city in each step, is called a greedy algorithm .

Finding an approximation to the shortest route in The Traveling Salesman Problem by always going to the nearest unvisited neighbor (greedy algorithm).

As you can see by running this simulation a few times, the routes that are found are not completely unreasonable. Except for a few times when the lines cross perhaps, especially towards the end of the algorithm, the resulting route is a lot shorter than we would get by choosing the next city at random.

Finding a near-optimal solution to the Traveling Salesman Problem using the nearest-neighbor algorithm (greedy):

Other Algorithms That Find Near-Optimal Solutions to The Traveling Salesman Problem

In addition to using a greedy algorithm to solve the Traveling Salesman Problem, there are also other algorithms that can find approximations to the shortest route.

These algorithms are popular because they are much more effective than to actually check all possible solutions, but as with the greedy algorithm above, they do not find the overall shortest route.

Algorithms used to find a near-optimal solution to the Traveling Salesman Problem include:

• 2-opt Heuristic: An algorithm that improves the solution step-by-step, in each step removing two edges and reconnecting the two paths in a different way to reduce the total path length.
• Genetic Algorithm: This is a type of algorithm inspired by the process of natural selection and use techniques such as selection, mutation, and crossover to evolve solutions to problems, including the TSP.
• Simulated Annealing: This method is inspired by the process of annealing in metallurgy. It involves heating and then slowly cooling a material to decrease defects. In the context of TSP, it's used to find a near-optimal solution by exploring the solution space in a way that allows for occasional moves to worse solutions, which helps to avoid getting stuck in local minima.
• Ant Colony Optimization: This algorithm is inspired by the behavior of ants in finding paths from the colony to food sources. It's a more complex probabilistic technique for solving computational problems which can be mapped to finding good paths through graphs.

Time Complexity for Solving The Traveling Salesman Problem

To get a near-optimal solution fast, we can use a greedy algorithm that just goes to the nearest unvisited city in each step, like in the second simulation on this page.

Solving The Traveling Salesman Problem in a greedy way like that, means that at each step, the distances from the current city to all other unvisited cities are compared, and that gives us a time complexity of \(O(n^2) \).

But finding the shortest route of them all requires a lot more operations, and the time complexity for that is \(O(n!)\), like mentioned earlier, which means that for 4 cities, there are 4! possible routes, which is the same as \(4 \cdot 3 \cdot 2 \cdot 1 = 24\). And for just 12 cities for example, there are \(12! = 12 \cdot 11 \cdot 10 \cdot \; ... \; \cdot 2 \cdot 1 = 479,001,600\) possible routes!

See the time complexity for the greedy algorithm \(O(n^2)\), versus the time complexity for finding the shortest route by comparing all routes \(O(n!)\), in the image below.

But there are two things we can do to reduce the number of routes we need to check.

In the Traveling Salesman Problem, the route starts and ends in the same place, which makes a cycle. This means that the length of the shortest route will be the same no matter which city we start in. That is why we have chosen a fixed city to start in for the simulation above, and that reduces the number of possible routes from \(n!\) to \((n-1)!\).

Also, because these routes go in cycles, a route has the same distance if we go in one direction or the other, so we actually just need to check the distance of half of the routes, because the other half will just be the same routes in the opposite direction, so the number of routes we need to check is actually \( \frac{(n-1)!}{2}\).

But even if we can reduce the number of routes we need to check to \( \frac{(n-1)!}{2}\), the time complexity is still \( O(n!)\), because for very big \(n\), reducing \(n\) by one and dividing by 2 does not make a significant change in how the time complexity grows when \(n\) is increased.

To better understand how time complexity works, go to this page .

Actual Traveling Salesman Problems Are More Complex

The edge weight in a graph in this context of The Traveling Salesman Problem tells us how hard it is to go from one point to another, and it is the total edge weight of a route we want to minimize.

So far on this page, the edge weight has been the distance in a straight line between two points. And that makes it much easier to explain the Traveling Salesman Problem, and to display it.

But in the real world there are many other things that affects the edge weight:

• Obstacles: When moving from one place to another, we normally try to avoid obstacles like trees, rivers, houses for example. This means it is longer and takes more time to go from A to B, and the edge weight value needs to be increased to factor that in, because it is not a straight line anymore.
• Transportation Networks: We usually follow a road or use public transport systems when traveling, and that also affects how hard it is to go (or send a package) from one place to another.
• Traffic Conditions: Travel congestion also affects the travel time, so that should also be reflected in the edge weight value.
• Legal and Political Boundaries: Crossing border for example, might make one route harder to choose than another, which means the shortest straight line route might be slower, or more costly.
• Economic Factors: Using fuel, using the time of employees, maintaining vehicles, all these things cost money and should also be factored into the edge weights.

As you can see, just using the straight line distances as the edge weights, might be too simple compared to the real problem. And solving the Traveling Salesman Problem for such a simplified problem model would probably give us a solution that is not optimal in a practical sense.

It is not easy to visualize a Traveling Salesman Problem when the edge length is not just the straight line distance between two points anymore, but the computer handles that very well.

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Top Tutorials

Top references, top examples, get certified.

Traveling salesman problem

This web page is a duplicate of https://optimization.mccormick.northwestern.edu/index.php/Traveling_salesman_problems

Author: Jessica Yu (ChE 345 Spring 2014)

Steward: Dajun Yue, Fengqi You

The traveling salesman problem (TSP) is a widely studied combinatorial optimization problem, which, given a set of cities and a cost to travel from one city to another, seeks to identify the tour that will allow a salesman to visit each city only once, starting and ending in the same city, at the minimum cost. 1

• 2.1 Graph Theory
• 2.2 Classifications of the TSP
• 2.3 Variations of the TSP
• 3.1 aTSP ILP Formulation
• 3.2 sTSP ILP Formulation
• 4.1 Exact algorithms
• 4.2.1 Tour construction procedures
• 4.2.2 Tour improvement procedures
• 5 Applications
• 7 References

The origins of the traveling salesman problem are obscure; it is mentioned in an 1832 manual for traveling salesman, which included example tours of 45 German cities but gave no mathematical consideration. 2 W. R. Hamilton and Thomas Kirkman devised mathematical formulations of the problem in the 1800s. 2

It is believed that the general form was first studied by Karl Menger in Vienna and Harvard in the 1930s. 2,3

Hassler Whitney, who was working on his Ph.D. research at Harvard when Menger was a visiting lecturer, is believed to have posed the problem of finding the shortest route between the 48 states of the United States during either his 1931-1932 or 1934 seminar talks. 2 There is also uncertainty surrounding the individual who coined the name “traveling salesman problem” for Whitney’s problem. 2

The problem became increasingly popular in the 1950s and 1960s. Notably, George Dantzig, Delber R. Fulkerson, and Selmer M. Johnson at the RAND Corporation in Santa Monica, California solved the 48 state problem by formulating it as a linear programming problem. 2 The methods described in the paper set the foundation for future work in combinatorial optimization, especially highlighting the importance of cutting planes. 2,4

In the early 1970s, the concept of P vs. NP problems created buzz in the theoretical computer science community. In 1972, Richard Karp demonstrated that the Hamiltonian cycle problem was NP-complete, implying that the traveling salesman problem was NP-hard. 4

Increasingly sophisticated codes led to rapid increases in the sizes of the traveling salesman problems solved. Dantzig, Fulkerson, and Johnson had solved a 48 city instance of the problem in 1954. 5 Martin Grötechel more than doubled this 23 years later, solving a 120 city instance in 1977. 5 Enoch Crowder and Manfred W. Padberg again more than doubled this in just 3 years, with a 318 city solution. 5

In 1987, rapid improvements were made, culminating in a 2,392 city solution by Padberg and Giovanni Rinaldi. In the following two decades, David L. Appelgate, Robert E. Bixby, Vasek Chvátal, & William J. Cook led the cutting edge, solving a 7,397 city instance in 1994 up to the current largest solved problem of 24,978 cities in 2004. 5

Description

Graph theory.

In the context of the traveling salesman problem, the verticies correspond to cities and the edges correspond to the path between those cities. When modeled as a complete graph, paths that do not exist between cities can be modeled as edges of very large cost without loss of generality. 6 Minimizing the sum of the costs for Hamiltonian cycle is equivalent to identifying the shortest path in which each city is visiting only once.

Classifications of the TSP

The TRP can be divided into two classes depending on the nature of the cost matrix. 3,6

• Applies when the distance between cities is the same in both directions

• Applies when there are differences in distances (e.g. one-way streets)

An ATSP can be formulated as an STSP by doubling the number of nodes. 6

Variations of the TSP

Formulation

The objective function is then given by

To ensure that the result is a valid tour, several contraints must be added. 1,3

There are several other formulations for the subtour elimnation contraint, including circuit packing contraints, MTZ constraints, and network flow constraints.

aTSP ILP Formulation

The integer linear programming formulation for an aTSP is given by

sTSP ILP Formulation

The symmetric case is a special case of the asymmetric case and the above formulation is valid. 3, 6 The integer linear programming formulation for an sTSP is given by

Exact algorithms

Branch-and-bound algorithms are commonly used to find solutions for TSPs. 7 The ILP is first relaxed and solved as an LP using the Simplex method, then feasibility is regained by enumeration of the integer variables. 7

Other exact solution methods include the cutting plane method and branch-and-cut. 8

Heuristic algorithms

Given that the TSP is an NP-hard problem, heuristic algorithms are commonly used to give a approximate solutions that are good, though not necessarily optimal. The algorithms do not guarantee an optimal solution, but gives near-optimal solutions in reasonable computational time. 3 The Held-Karp lower bound can be calculated and used to judge the performance of a heuristic algorithm. 3

There are two general heuristic classifications 7 :

• Tour construction procedures where a solution is gradually built by adding a new vertex at each step
• Tour improvement procedures where a feasbile solution is improved upon by performing various exchanges

The best methods tend to be composite algorithms that combine these features. 7

Tour construction procedures

Tour improvement procedures

Applications

The importance of the traveling salesman problem is two fold. First its ubiquity as a platform for the study of general methods than can then be applied to a variety of other discrete optimization problems. 5 Second is its diverse range of applications, in fields including mathematics, computer science, genetics, and engineering. 5,6

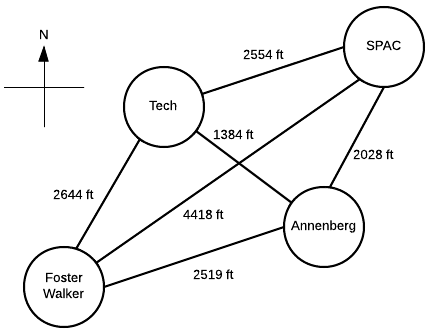
Suppose a Northwestern student, who lives in Foster-Walker , has to accomplish the following tasks:

• Drop off a homework set at Tech
• Work out a SPAC
• Complete a group project at Annenberg

Distances between buildings can be found using Google Maps. Note that there is particularly strong western wind and walking east takes 1.5 times as long.

It is the middle of winter and the student wants to spend the least possible time walking. Determine the path the student should take in order to minimize walking time, starting and ending at Foster-Walker.

Start with the cost matrix (with altered distances taken into account):

Method 1: Complete Enumeration

All possible paths are considered and the path of least cost is the optimal solution. Note that this method is only feasible given the small size of the problem.

From inspection, we see that Path 4 is the shortest. So, the student should walk 2.28 miles in the following order: Foster-Walker → Annenberg → SPAC → Tech → Foster-Walker

Method 2: Nearest neighbor

Starting from Foster-Walker, the next building is simply the closest building that has not yet been visited. With only four nodes, this can be done by inspection:

• Smallest distance is from Foster-Walker is to Annenberg
• Smallest distance from Annenberg is to Tech
• Smallest distance from Tech is to Annenberg ( creates a subtour, therefore skip )
• Next smallest distance from Tech is to Foster-Walker ( creates a subtour, therefore skip )
• Next smallest distance from Tech is to SPAC
• Smallest distance from SPAC is to Annenberg ( creates a subtour, therefore skip )
• Next smallest distance from SPAC is to Tech ( creates a subtour, therefore skip )
• Next smallest distance from SPAC is to Foster-Walker

So, the student would walk 2.54 miles in the following order: Foster-Walker → Annenberg → Tech → SPAC → Foster-Walker

Method 3: Greedy

With this method, the shortest paths that do not create a subtour are selected until a complete tour is created.

• Smallest distance is Annenberg → Tech
• Next smallest is SPAC → Annenberg
• Next smallest is Tech → Annenberg ( creates a subtour, therefore skip )
• Next smallest is Anneberg → Foster-Walker ( creates a subtour, therefore skip )
• Next smallest is SPAC → Tech ( creates a subtour, therefore skip )
• Next smallest is Tech → Foster-Walker
• Next smallest is Annenberg → SPAC ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → Annenberg ( creates a subtour, therefore skip )
• Next smallest is Tech → SPAC ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → Tech ( creates a subtour, therefore skip )
• Next smallest is SPAC → Foster-Walker ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → SPAC

So, the student would walk 2.40 miles in the following order: Foster-Walker → SPAC → Annenberg → Tech → Foster-Walker

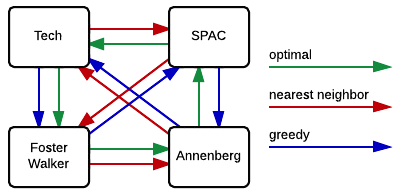
As we can see in the figure to the right, the heuristic methods did not give the optimal solution. That is not to say that heuristics can never give the optimal solution, just that it is not guaranteed.

Both the optimal and the nearest neighbor algorithms suggest that Annenberg is the optimal first building to visit. However, the optimal solution then goes to SPAC, while both heuristic methods suggest Tech. This is in part due to the large cost of SPAC → Foster-Walker. The heuristic algorithms cannot take this future cost into account, and therefore fall into that local optimum.

We note that the nearest neighbor and greedy algorithms give solutions that are 11.4% and 5.3%, respectively, above the optimal solution. In the scale of this problem, this corresponds to fractions of a mile. We also note that neither heuristic gave the worst case result, Foster-Walker → SPAC → Tech → Annenberg → Foster-Walker.

Only tour building heuristics were used. Combined with a tour improvement algorithm (such as 2-opt or simulated annealing), we imagine that we may be able to locate solutions that are closer to the optimum.

The exact algorithm used was complete enumeration, but we note that this is impractical even for 7 nodes (6! or 720 different possibilities). Commonly, the problem would be formulated and solved as an ILP to obtain exact solutions.

• Vanderbei, R. J. (2001). Linear programming: Foundations and extensions (2nd ed.). Boston: Kluwer Academic.
• Schrijver, A. (n.d.). On the history of combinatorial optimization (till 1960).
• Matai, R., Singh, S., & Lal, M. (2010). Traveling salesman problem: An overview of applications, formulations, and solution approaches. In D. Davendra (Ed.), Traveling Salesman Problem, Theory and Applications . InTech.
• Junger, M., Liebling, T., Naddef, D., Nemhauser, G., Pulleyblank, W., Reinelt, G., Rinaldi, G., & Wolsey, L. (Eds.). (2009). 50 years of integer programming, 1958-2008: The early years and state-of-the-art surveys . Heidelberg: Springer.
• Cook, W. (2007). History of the TSP. The Traveling Salesman Problem . Retrieved from http://www.math.uwaterloo.ca/tsp/history/index.htm
• Punnen, A. P. (2002). The traveling salesman problem: Applications, formulations and variations. In G. Gutin & A. P. Punnen (Eds.), The Traveling Salesman Problem and its Variations . Netherlands: Kluwer Academic Publishers.
• Laporte, G. (1992). The traveling salesman problem: An overview of exact and approximate algorithms. European Journal of Operational Research, 59 (2), 231–247.
• Goyal, S. (n.d.). A suvey on travlling salesman problem.

Navigation menu

• Travelling salesman problem

The travelling salesman problem (often abbreviated to TSP) is a classic problem in graph theory . It has many applications, in many fields. It also has quite a few different solutions.

The problem

The problem is usually stated in terms of a salesman who needs to visit several towns before eventually returning to the starting point. There are various routes he could take, visiting the different towns in different orders. Here is an example:

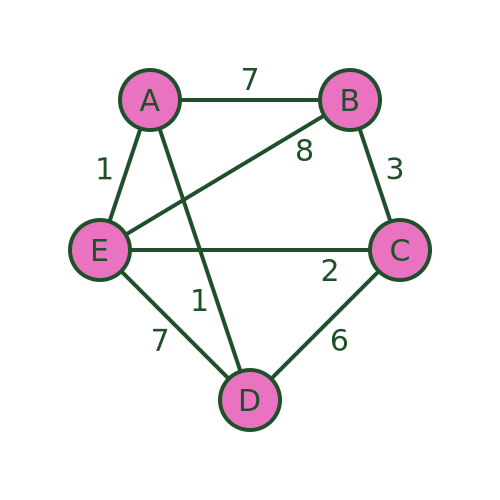
There are several different routes that will visit every town. For example, we could visit the towns in the order A , B , C , D , E , then back to A . Or we could use the route A , D , C , E , B then back to A .

But not all routes are possible. For example, we cannot use a route A , D , E , B , C and then back to A , because there is no road from C to A .

The aim is to find the route that visits all the towns with the minimum cost . The cost is shown as the weight of each edge in the graph. This might be the distance between the towns, or it might be some other measure. For example, it might be the time taken to travel between the towns, which might not be proportionate to the distance because some roads have lower speed limits or are more congested. Or, if the salesman was travelling by train, it might be the price of the tickets.

The salesman can decide to optimise for whatever measure he considers to be most important.

Alternative applications and variants

TSP applies to any problem that involves visiting various places in sequence. One example is a warehouse, where various items need to be fetched from different parts of a warehouse to collect the items for an order. In the simplest case, where one person fetches all the items for a single order and then packs and dispatches the items, a TSP algorithm can be used. Of course, a different route would be required for each order, which would be generated by the ordering system.

Another interesting example is printed circuit board (PCB) drilling. A PCB is the circuit board you will find inside any computer or other electronic device. They often need holes drilled in them, including mounting holes where the board is attached to the case and holes where component wires need to pass through the board. These holes are usually drilled by a robot drill that moves across the board to drill each hole in the correct place. TSP can be used to calculate the optimum drilling order.

The TSP algorithm can be applied to directed graphs (where the distance from A to B might be different to the distance from B to A ). Directed graphs can represent things like one-way streets (where the distance might not be the same in both directions) or flight costs (where the price of a single airline ticket might not be the same in both directions).

There are some variants of the TSP scenario. The mTSP problem covers the situation where there are several salesmen and exactly one salesman must visit each city. This applies to delivery vans, where there might be several delivery vans. The problem is to decide which parcels to place on each van and also to decide the route of each van.

The travelling purchaser problem is another variant. In that case, a purchaser needs to buy several items that are being sold in different places, potentially at different prices. The task is to purchase all the items, minimising the total cost (the cost of the items and the cost of travel). A simple approach would be to buy each item from the place where it is cheapest, in which case this becomes a simple TSP. However, it is not always worth buying every item from the cheapest place because sometimes the travel cost might outweigh the price difference.

In this article, we will only look at the basic TSP case.

Brute force algorithm

We will look at 3 potential algorithms here. There are many others. The first, and simplest, is the brute force approach.

We will assume that we start at vertex A . Since we intend to make a tour of the vertices (ie visit every vertex once and return to the original vertex) it doesn't matter which vertex we start at, the shortest loop will still be the same.

So we will start at A , visit nodes B , C , D , and E in some particular order, then return to A .

To find the shortest route, we will try every possible ordering of vertices B , C , D , E , and record the cost of each one. Then we can find the shortest.

For example, the ordering ABCDEA has a total cost of 7+3+6+7+1 = 24.

The ordering ABCEDA (i.e. swapping D and E ) has a total cost of 7+3+2+7+1 = 20.

Some routes, such as ADEBCA are impossible because a required road doesn't exist. We can just ignore those routes.

After evaluating every possible route, we are certain to find the shortest route (or routes, as several different routes may happen to have the same length that also happens to be the shortest length). In this case, the shortest route is AECBDA with a total length of 1+8+3+6+1 = 19.

The main problem with this algorithm is that it is very inefficient. In this example, since we have already decided that A is the start/end point, we must work out the visiting order for the 4 towns BCDE . We have 4 choices of the first town, 3 choices for the second town, 2 choices for the third town, and 1 choice for the fourth town. So there are 4! (factorial) combinations. That is only 24 combinations, which is no problem, you could even do it by hand.

If we had 10 towns (in addition to the home town) there would be 10! combinations, which is 3628800. Far too many to do by hand, but a modern PC might be able to do that in a fraction of a second if the algorithm was implemented efficiently.

If we had 20 towns, then the number of combinations would be of order 10 to the power 18. If we assume a computer that could evaluate a billion routes per second (which a typical PC would struggle to do, at least at the time of writing), that would take a billion seconds, which is several decades.

Of course, there are more powerful computers available, and maybe quantum computing will come into play soon, but that is only 20 towns. If we had 100 towns, the number of combinations would be around 10 to the power 157, and 1000 towns 10 to the power 2568. For some applications, it would be quite normal to have hundreds of vertices. The brute force method is impractical for all but the most trivial scenarios.

Nearest neighbour algorithm

The nearest neighbour algorithm is what we might call a naive attempt to find a good route with very little computation. The algorithm is quite simple and obvious, and it might seem like a good idea to someone who hasn't put very much thought into it. You start by visiting whichever town is closest to the starting point. Then each time you want to visit the next town, you look at the map and pick the closest town to wherever you happen to be (of course, you will ignore any towns that you have visited already). What could possibly go wrong?

Starting at A , we visit the nearest town that we haven't visited yet. In this case D and E are both distance 1 from A . We will (completely arbitrarily) always prioritise the connections in alphabetical order. So we pick D .

As an aside, if we had picked E instead we would get a different result. It might be better, but it is just as likely to be worse, so there is no reason to chose one over the other.

From D , the closest town is C with a distance of 6 (we can't pick A because we have already been there).

From C the closest town is E with distance 2. From E we have to go to B because we have already visited every other town - that is a distance of 8. And from B we must return to A with a distance of 7.

The final path is ADCEBA and the total distance is 1+6+2+8+7 = 24.

The path isn't the best, but it isn't terrible. This algorithm will often find a reasonable path, particularly if there is a natural shortest path. However, it can sometimes go badly wrong.

The basic problem is that the algorithm doesn't take account of the big picture. It just blindly stumbles from one town to whichever next town is closest.

In particular, the algorithm implicitly decides that the final step will be B to A . It does this based on the other distances, but without taking the distance BA into account. But what if, for example, there is a big lake between B and A that you have to drive all the way around? This might make the driving distance BA very large. A more sensible algorithm would avoid that road at all costs, but the nearest neighbour algorithm just blindly leads us there.

We can see this with this revised graph where BA has a distance of 50:

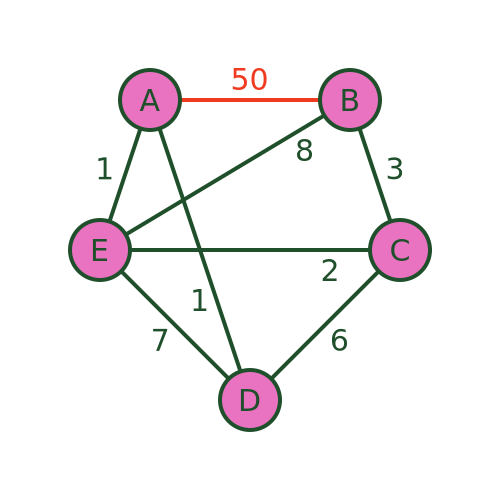
The algorithm will still recommend the same path because it never takes the distance BA into account. The path is still ADCEBA but the total distance is now 1+6+2+8+50 = 67. There are much better routes that avoid BA .

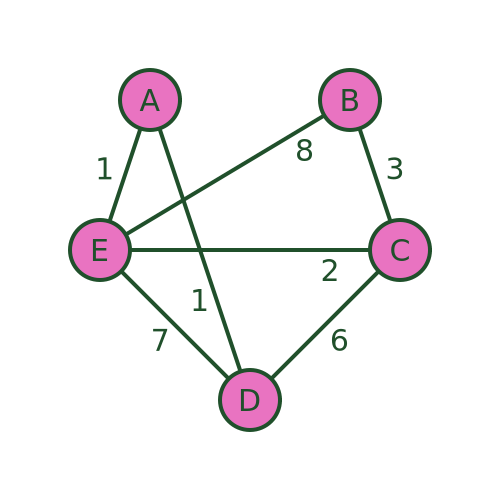
An even worse problem can occur if there is no road at all from B to A . The algorithm would still guide us to town B as the final visit. But in that case, it is impossible to get from B to A to complete the journey:

Bellman–Held–Karp algorithm

The Bellman–Held–Karp algorithm is a dynamic programming algorithm for solving TSP more efficiently than brute force. It is sometimes called the Held–Karp algorithm because it was discovered by Michael Held and Richard Karp, but it was also discovered independently by Richard Bellman at about the same time.

The algorithm assumes a complete graph (ie a graph where every vertex is connected to every other). However, it can be used with an incomplete graph like the one we have been using. To do this, we simply add extra the missing connections (shown below in grey) and assign them a very large distance (for example 1000). This ensures that the missing connections will never form part of the shortest path:

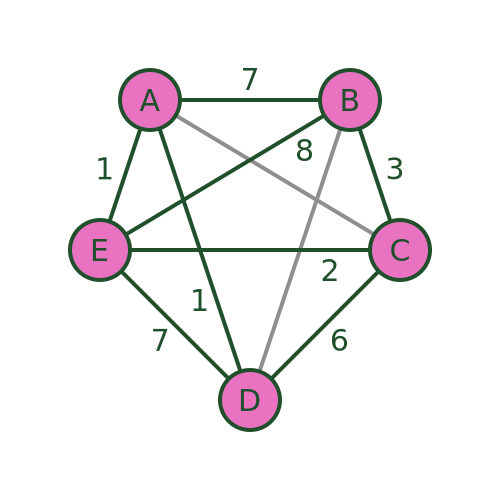
The technique works by incrementally calculating the shortest path for every possible set of 3 towns (starting from A ), then for every possible set of 4 towns, and so on until it eventually calculates the shortest path that goes from A via every other town and back to A .

Because the algorithm stores its intermediate calculations and discards non-optimal paths as early as possible, it is much more efficient than brute force.

We will use the following notation. We will use this to indicate the distance between towns A and B :

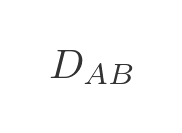
And we will use this to indicate the cost (ie the total distance) from A to C via B :

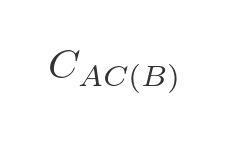
Here are some examples:

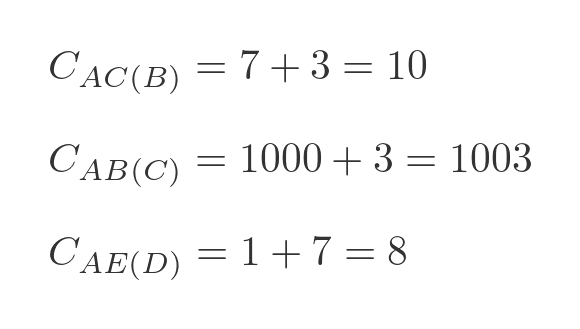
The first example is calculated by adding the distance AB to BC , which gives 10. The second example is calculated by adding AC to CB . But since there is no road from A to C , we give that a large dummy distance of 1000, so that total cost is 1003, which means it is never going to form a part of the shortest route. The third example is calculated by adding the distance AD to DE , which gives 8.

In the first step, we will calculate the value of every possible combination of 2 towns starting from A . There are 12 combinations: AB(C) , AB(D) , AB(E) , AC(B) , AC(D) , AC(E) , AD(B) , AD(C) , AD(E) , AE(B) , AE(C) , AE(D) .

These values will be stored for later use.

For step 2 we need to extend our notation slightly. We will use this to indicate the lowest cost from A to D via B and C (in either order):

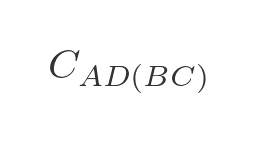
To be clear, this could represent one of two paths - ABCD or ACBD whichever is shorter. We can express this as a minimum of two values:

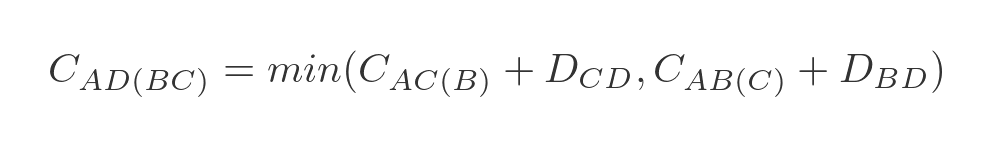
This represents the 2 ways to get from A to D via B and C :

• We can travel from A to C via B , and then from C to D .
• We can travel from A to B via C , and then from B to D .

We have already calculated A to C via B (and all the other combinations) in step 1, so all we need to do is add the values and find the smallest. In this case:

• A to C via B is 10, C to D is 6, so the total is 16.
• A to B via C is 1003, B to D is 1000, so the total is 2003.

Clearly, ABCD is the best route.

We need to repeat this for every possible combination of travelling from A to x via y and z . There are, again, 12 combinations: AB(CD) , AB(CE) , AB(DE) , AC(BD) , AC(BE) , AC(DE) , AD(BC) , AD(BE) , AD(CE) , AE(BC) , AE(BD) , AE(CD) .

We store these values, along with the optimal path, for later use.

In the next step, we calculate the optimal route for travelling from A to any other town via 3 intermediate towns. For example, travelling from A to E via B , C , and D (in the optimal order) is written as:

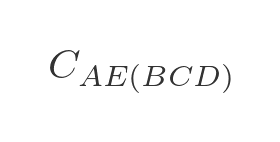
There are 3 paths to do this:

• A to D via B and C , then from D to E .
• A to C via B and D , then from C to E .
• A to B via C and D , then from B to E .

We will choose the shortest of these three paths:

Again we have already calculated all the optimal intermediate paths. This time there are only 4 combinations we need to calculate: AB(CDE) , AC(BDE) , AD(BCE) , and AE(BCD) .

We are now in a position to calculate the optimal route for travelling from A back to A via all 4 other towns:

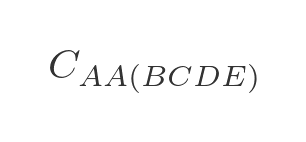
We need to evaluate each of the 4 options in step 3, adding on the extra distance to get back to A :

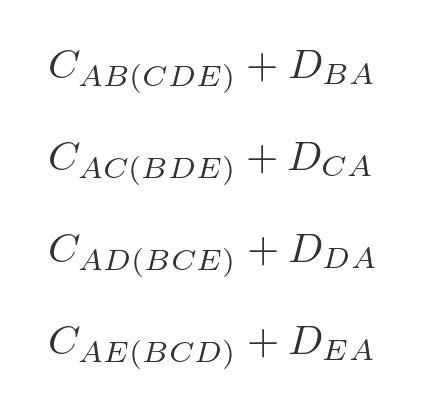
We can then choose the option that has the lowest total cost, and that will be the optimal route.

Performance

The performance of the Bellman–Held–Karp algorithm can be expressed in big-O notations as:

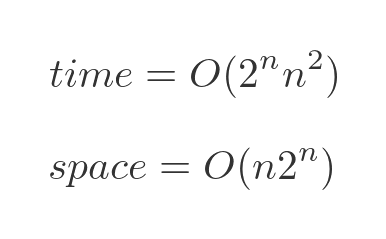
The time performance is approximately exponential. As the number of towns increases, the time taken will go up exponentially - each time an extra town is added, the time taken will double. We are ignoring the term in n squared because the exponential term is the most significant part.

Exponential growth is still quite bad, but it is far better than the factorial growth of the brute-force algorithm.

It is also important to notice that the algorithm requires memory to store the intermediate results, which also goes up approximately exponentially. The brute force algorithm doesn't have any significant memory requirements. However, that is usually an acceptable trade-off for a much better time performance.

The stages above describe how the algorithm works at a high level. We haven't gone into great detail about exactly how the algorithm keeps track of the various stages. Over the years since its discovery, a lot of work has been put into optimising the implementation. Optimising the implementation won't change the time complexity, which will still be roughly exponential. However, it might make the algorithm run several times faster than a poor implementation.

We won't cover this in detail, but if you ever need to use this algorithm for a serious purpose, it is worth considering using an existing, well-optimised implementation rather than trying to write it yourself. Unless you are just doing it for fun!

Other algorithms

Even the Bellman–Held–Karp algorithm has poor performance for modestly large numbers of towns. 100 towns, for example, would be well beyond the capabilities of a modern PC.

There are various heuristic algorithms that are capable of finding a good solution, but not necessarily the best possible solution, in a reasonable amount of time. I hope to cover these in a future article.

• Adjacency matrices
• The seven bridges of Königsberg
• Permutation matrices and graphs
• Dijkstra's algorithm

Join the GraphicMaths Newletter

Sign up using this form to receive an email when new content is added:

Popular tags

adder adjacency matrix alu and gate angle area argand diagram binary maths cartesian equation chain rule chord circle cofactor combinations complex modulus complex polygon complex power complex root cosh cosine cosine rule cpu cube decagon demorgans law derivative determinant diagonal directrix dodecagon eigenvalue eigenvector ellipse equilateral triangle euler eulers formula exponent exponential exterior angle first principles flip-flop focus gabriels horn gradient graph hendecagon heptagon hexagon horizontal hyperbola hyperbolic function hyperbolic functions infinity integration by parts integration by substitution interior angle inverse hyperbolic function inverse matrix irrational irregular polygon isosceles trapezium isosceles triangle kite koch curve l system line integral locus maclaurin series major axis matrix matrix algebra mean minor axis nand gate newton raphson method nonagon nor gate normal normal distribution not gate octagon or gate parabola parallelogram parametric equation pentagon perimeter permutations polar coordinates polynomial power probability probability distribution product rule proof pythagoras proof quadrilateral radians radius rectangle regular polygon rhombus root sech set set-reset flip-flop sine sine rule sinh sloping lines solving equations solving triangles square standard curves standard deviation star polygon statistics straight line graphs surface of revolution symmetry tangent tanh transformation transformations trapezium triangle turtle graphics variance vertical volume volume of revolution xnor gate xor gate

• Graph theory
• 7 bridges of Königsberg
• Binary numbers

• CMPT 125 Summer 2012 1 documentation »

13. Case Study: Solving the Traveling Salesman Problem ¶

13.1. the problem ¶.

The traveling salesman problem , referred to as the TSP , is one of the most famous problems in all of computer science. It’s a problem that’s easy to describe, yet fiendishly difficult to solve. In fact, it remains an open question as to whether or not it is possible to efficiently solve all TSP instances.

Here is the problem. Suppose you are a salesman travelling that has a list of cities that you want to visit. You want to go to each city exactly once. Naturally, you want to tour all the cities in the order that requires traveling the shortest distance.

For instance, suppose you’re visiting these four cities:

You always start, and end, at 0, your home city. We assume the following distances between cities:

dist(0, 1) = 10 dist(0, 2) = 10 dist(0, 3) = 14 dist(1, 2) = 14 dist(1, 3) = 10 dist(2, 3) = 10

In this case the distances are symmetric , i.e. dist(a, b) is always the same as dist(b, a). So for example we know dist(3, 2) = 10 because we are told dist(2, 3) = 10.

Here are some different tours of the cities:

0 to 1 to 3 to 2 (and back to 0); total distance = 10 + 10 + 10 + 10 = 40

0 to 2 to 3 to 1 (and back to 0); total distance = 10 + 10 + 10 + 10 = 40

0 to 3 to 1 to 2 (and back to 0); total distance = 14 + 10 + 14 10 = 48

0 to 2 to 1 to 3 (and back to 0); total distance = 10 + 14 + 10 + 14 = 48

Clearly, some tours are shorter than others. For this small 4-city example it is easy to see that the shortest way to visit all the cities is to go around the edges and avoid the long diagonals.

But not all instances of the TSP are so simple or so small. For instance, suppose you want to visit all 4600-plus Canadian cities. It is not at all obvious how you should go about finding the shortest possible tour of so many cities.

13.2. The Simplest Solution: Brute Force ¶

If you think about it, representing a TSP tour is not too hard: it is just a permutation of the cities, with the added restriction that the first city must always be 0 (your home city). For instance, we can write the above tours compactly like this:

0, 2, 3, 2 0, 2, 3, 1 0, 3, 1, 2 0, 2, 1, 3

Once we realize a tour is a permutation, then a brute-force algorithm that is guaranteed to always solve the TSP becomes evident:

Brute-force algorithm : Examine all possible permutations of cities, and keep the one that is shortest.

13.3. Planning Our Program ¶

Lets give some thought to the overall structure and organization of our program.

First, we will assume that the cities are named 0 to n - 1, and that a tour of these n cities is a permutation of the numbers from 0 to n - 1. We assume that 0 is the home city, and that all tours start with 0.

Second, we need some way to store the cities. Since our cities are on a 2-dimensional map, we can store them as (x, y) points using the Point class from previous notes . We’ll store the cities as a vector<Point> , where each city’s name is the same as its index number in the vector , i.e. the city at index location 0 is named 0, the city at index location 1 is named 1, and so on.

We’re also going to need a function to calculate the distance between two cities, and another function to calculate the total length of a tour of cities. So lets write a class called Tsp_map whose responsibility is to take care of such details. A Tsp_map object will store a collection of cities, provide functions for calculating distances, and maybe some other helper functions as well.

Recall from math class that distance between the points (x, y) and (a, b) is given by this formula:

Third, lets agree to represent a tour (i.e. a permutation of city names) as a vector<int> . The numbers in it represent the names of the cities in a particular Tsp_map , and the order of the numbers is the order in which the cities will be visited.

13.4. The Tsp_map Class ¶

Using the above notes as a guide, lets start to write the Tsp_map class:

Note the following:

The variable cities is of type vector<Point> , and it stores a list of cities as Point objects.

We’ve declared cities to be private as a matter of good design: by default, all variables in a class should be private unless there is a clear reason for making them public.

No constructor has been written for this function because no special initialization is need. C++ automatically initializes cities to be empty when a Tsp_map object is created.

Two add functions are provided for adding cities to the Tsp_map . Note that one calls the other.

The dist_between functions takes the names (i.e. index locations) of two cities and returns the distance between them using the dist function from Point.h . If either of the parameters i or j is not a legal name of a city, then an error will be thrown because cities is a checked_vector .

The score functions calculates the total length of a given tour. Note that the distance between the first city and last city is included.

The get_default_tour function is a handy way to get a list of all the cities for a particular Tsp_map . It just returns a vector<int> initialized to 0, 1, 2, 3, ..., n - 1.

size , dist_between , score , and get_default_tour have all been declared const functions. In general, you should always declare functions in class to be const if possible. That way they will work with const Tsp_map objects.

The two add functions are not declared const because they modify cities .

We can use a Tsp_map like this:

13.5. Using typedef to Make a Type Synonym ¶

Our tours are represented as plain vector<int> objects. A problem with this is that writing vector<int> all the time is a bit tedious, and it also doesn’t clearly indicate that it is being used to represent a tour. So we what we can do is to use typedef to create a synonym for vector<int> with a more descriptive name:

Now we can write Tour instead of vector<int> :

This makes the purpose of the code clearer, and clearer code is always a good thing.

13.6. The Brute Force Solving Function ¶

Now lets write a function that uses brute force to solve a TSP problem. The header will look like this:

This is not inside the Tsp_map function. Instead, it is a stand-alone function that takes a Tsp_map as input.

In pseudocode, the brute force algorithm goes like this:

get an initial tour; call it T best_tour ⇦ T best_score ⇦ score(T) while there are more permutations of T do the following generate a new permutation of T if score(T) < best_score then best_tour ⇦ T best_score ⇦ score(T) print best_tour and best_score

As is often done in pseudocode, we use an arrow “⇦” to indicate variable assignment. The reason for this is that it is more suggestive than “=”, plus it lets us use “=” in the usual mathematical way in pseudocode if we need it.

The next step is to convert the pseudocode to C++:

The most interesting detail here is how the permutations are generated. It turns out that the C++ standard template library (the STL) has a function called next_permutation that will re-arrange the elements of a sequence to the next permutation in lexicographic order .

Lexicographic order is a generalization of alphabetical order that works with numbers. By starting with the permutation 0, 1, 2, ..., n - 1, next_permutation guarantees to cycle through all possible permutations, returning false when it as the last one.

Notice that we pass in tour.begin() + 1 instead of tour.begin() :

That’s because we know, from our definition of the problem, that the first element of a tour should always be 0. Thus we only need to permute the n - 1 numbers after 0.

13.7. The Problem with Solving the TSP by Brute Force ¶

Solving the TSP by brute force has a couple of important benefits:

• It is guaranteed to find a shortest tour through the cities.
• It is conceptually quite straightforward, i.e. it just looks at all possible tours and finds the shortest one.

For small number of cities the brute-force solver works well. For example:

In practice, no matter how fast your computer, or how many you have, you won’t be able to generate this many permutations in a reasonable amount of time.

13.8. Random Guessing ¶

If generating all permutations is too slow in practice, then lets try another extreme: generating permutations at random.

Random Tour Algorithm : Generate random tours, and save the shortest one. Stop when you have no more time left to search for tours.

The code for this algorithm is very similar to the code for generating all permutations:

As with the brute-force solver, we use best_score and best_tour to keep track of the shortest tour seen so far. Each time through the for-loop, the tour cities are shuffled using the standard random_shuffle algorithm, and then scored. If this shuffled tour is shorter than the shortest one seen so far, it’s saved.

It’s up to the programmer to decided how many random guesses should be made. By default, a million random guesses are made, which runs in a couple of seconds on my computer.

However, for large TSP problems random guessing is terrible because it blindly takes permutations from a huge search space. It’s like searching for a needle in a giant haystack by randomly plucking out one straw at a time.

13.9. Better Algorithms ¶

As mentioned, the TSP is an extremely well-studied problem, and numerous fast algorithms that usually find pretty short (not always the shortest) tour have been created. As just one example of a better method, consider this algorithm for constructing a tour a city at a time:

• Start with city 0 in the tour
• Look at the last city in the tour, and then add to the end of the tour the closest city not already in it.
• Repeat the previous step until all cities have been added.

While this algorithm does not guarantee to always find a shortest possible tour, it is certainly better than random guessing, and fast enough to be applied to very large TSP instances.

It’s currently unknown if there is an algorithm that can always guarantee to efficiently find the shortest tour in any TSP. The majority of computer scientists probably believe that there is no such algorithm, but this has not been proved.

If you’d like to learn more about the TSP and how to solve it efficiently, a good starting place is this TSP page . One of the many interesting things on that page is an optimal tour of all of Canada’s 4,663 main cities.

13.10. Aside: An Example Where Brute Force Works Well ¶

Brute force doesn’t work well for the TSP, but for some problems it is a good solution method. For example, perhaps you have heard of “alphametic”, or “cryptarithm” puzzles like this:

Each letter of the puzzle stands for a single digit, and different letters must have different values. Also, letters at the start of a word can’t be 0.

A brute force solution to this puzzle work like this:

Create a vector v of 10 integers, initialized to 0, 1, 2, ..., 9. Since there are eight different letters in the puzzle, we only care about the first 8 elements of this vector, v[0] to v[7] .

Associate letters with elements in the vector, e.g.:

S is v[0] E is v[1] N is v[2] D is v[3] M is v[4] O is v[5] R is v[6] Y is v[7]

Here’s a program that solves the puzzle:

On my computer, this program takes 0.08 seconds to find two solutions:

These are actually the same solution since we only care about the first 8 digits; the last 2 are not used in this puzzle:

Table Of Contents

• 13.1. The Problem
• 13.2. The Simplest Solution: Brute Force
• 13.3. Planning Our Program
• 13.4. The Tsp_map Class
• 13.5. Using typedef to Make a Type Synonym
• 13.6. The Brute Force Solving Function
• 13.7. The Problem with Solving the TSP by Brute Force
• 13.8. Random Guessing
• 13.9. Better Algorithms
• 13.10. Aside: An Example Where Brute Force Works Well

Previous topic

12. Introduction to Object-oriented Programming (OOP)

14. Reading and Writing Streams

• Show Source

Quick search

Enter search terms or a module, class or function name.

• Coding Problems

Travelling Salesman Problem (TSP)

Problem statement, example 1: travelling salesman problem, example 2: travelling salesman problem, 1. simple approach, c++ code implementation, java code implementation, python code implementation, 2. travelling salesman problem using dynamic programming, c code implementation, 3. greedy approach, practice questions, frequently asked questions, 1. which algorithm is used for the travelling salesman problem, 2. what is the complexity of the travelling salesman problem, 3. how is this problem modelled as a graph problem, 4: what is the difficulty level of the travelling salesman problem.

Travelling Salesman Problem (TSP) – Given a set of cities and the distance between every pair of cities as an adjacency matrix, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. The ultimate goal is to minimize the total distance travelled, forming a closed tour or circuit.

The TSP is referred to as an NP-hard problem, meaning there is no known algorithm to solve it in polynomial time for large instances. As the number of cities increases, the number of potential solutions grows exponentially, making an exhaustive search unfeasible. This complexity is one of the reasons why the TSP remains a popular topic of research. Learn More .

Input –

Confused about your next job?

Output –

Here, the TSP Tour is 0-2-1-3-0 and the cost of the tour is 48.

Minimum weight Hamiltonian Cycle : EACBDE= 32

Wondering how the Hamiltonian Cycle Problem and the Traveling Salesman Problem differ? The Hamiltonian Cycle problem is to find out if there exists a tour that visits each city exactly once. Here, we know that the Hamiltonian Tour exists (due to the graph being complete), and there are indeed many such tours. The problem is to find a minimum weight Hamiltonian Cycle.

There are various approaches to finding the solution to the travelling salesman problem- simple (naïve) approach, dynamic programming approach, and greedy approach. Let’s explore each approach in detail:

• Consider city 1 as the starting and ending point. Since the route is cyclic, we can consider any point as a starting point.
• Now, we will generate all possible permutations of cities which are (n-1)!.
• Find the cost of each permutation and keep track of the minimum cost permutation.
• Return the permutation with minimum cost.
• Time complexity: O(N!), Where N is the number of cities.
• Space complexity: O(1).

In the travelling salesman problem algorithm, we take a subset N of the required cities that need to be visited, the distance among the cities dist, and starting cities s as inputs. Each city is identified by a unique city id which we say like 1,2,3,4,5………n

Here we use a dynamic approach to calculate the cost function Cost(). Using recursive calls, we calculate the cost function for each subset of the original problem.

To calculate the cost(i) using Dynamic Programming , we need to have some recursive relation in terms of sub-problems.

We start with all subsets of size 2 and calculate C(S, i) for all subsets where S is the subset, then we calculate C(S, i) for all subsets S of size 3 and so on.

There are at most O(n2^n) subproblems, and each one takes linear time to solve. The total running time is, therefore, O(n^22^n). The time complexity is much less than O(n!) but still exponential. The space required is also exponential.

• Time Complexity: O(N^2*2^N).
• First of them is a list that can hold the indices of the cities in terms of the input matrix of distances between cities
• And the Second one is the array which is our result
• Perform traversal on the given adjacency matrix tsp[][] for all the cities and if the cost of reaching any city from the current city is less than the current cost update the cost.
• Generate the minimum path cycle using the above step and return their minimum cost.
• Time complexity: O(N^2*logN), Where N is the number of cities.
• Space complexity: O(N).
• City Tour Problem
• Shortest Common Substring

Ans . Travelling Salesman Problem uses Dynamic programming with a masking algorithm.

Ans.: The complexity of TSP using Greedy will be O(N^2 LogN) and using DP will be O(N^2 2^N).

Ans .: The TSP can be modelled as a graph problem by considering a complete graph G = (V, E). A tour is then a circuit in G that meets every node. In this context, tours are sometimes called Hamiltonian circuits.

Ans.: It is an NP-hard problem.

• Travelling Salesman Problem

Previous Post

Top principles of scrum, difference between product and service based company.